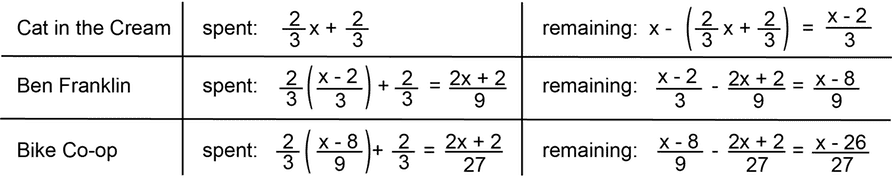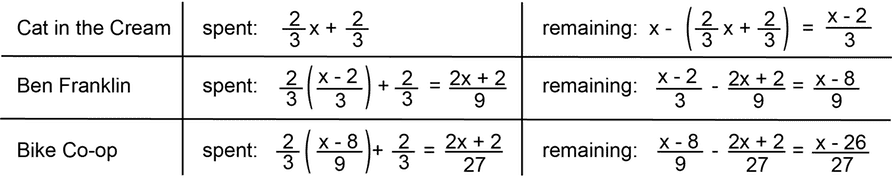1540.37 – Celeste in Obieland

Celeste bought some stuff from The-Cat-in-the-Cream (a coffee house), Ben Franklin (a dime store), and the bike co-op. At each place, she spent exactly 2/3 of her money plus 2/3 of a cent. When she was finished, she had exactly a dollar left. What was her original bankroll?

Solution

Let xx be the number of pennies Celeste started with. You can work from either end.

Starting at the beginning and working forwards, we find that xx satisfies the equation

x−2627=100.\frac{x-26}{27} = 100.

(See the table below!) It follows that x=2726x = 2726 pennies, so Celeste started with \27.26$.

Starting at the very end and working backwards, Celeste has:

100 pennies after visiting the Bike Co-op, 100 \text{ pennies after visiting the Bike Co-op,}

(100+23)⋅3=302 after Ben Franklin,\left( 100 + \frac{2}{3} \right) \cdot 3 = 302 \text{ after Ben Franklin,}

(302+23)⋅3=906 after The-Cat-in-the-Cream,\left( 302 + \frac{2}{3} \right) \cdot 3 = 906 \text{ after The-Cat-in-the-Cream,}

(906+23)⋅3=2726 initially.\left( 906 + \frac{2}{3} \right) \cdot 3 = 2726 \text{ initially.}

1540_37_solution_6717bba407.png