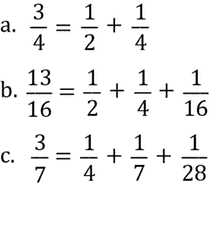1368.25 – Egyptian Fractions Intro

The Egyptians typically wrote fractions as sums of unit fractions, that is, fractions with numerator 1. With the exception of a few common simple fractions like 2/3, all non-unit fractions were taken apart in this way as sums of unit fractions. And the unit fractions had to be distinct, that is, the denominators had to be different.

For example:

\frac{3}{5}= \frac{1}{2}+\frac{1}{10}

\frac{5}{6}= \frac{1}{2}+\frac{1}{3}

Write these fractions as Egyptian fractions:

$\dfrac{3}{4}$
$\dfrac{13}{16}$
$\dfrac{3}{7}$

Solution

One systematic way to find Egyptian fractions is to find the largest unit fraction that is smaller than the given fraction. If the remainder is not itself a unit fraction, keep repeating this process until you have a sum of unit fractions.