1310.25 – Super Venn Diagram

In the diagram below are ten overlapping circles, each identified by a letter. There are pebbles in each circle. Each unique letter corresponds to a different whole number of pebbles, from one to nine, but the two circles labeled with $H$ will have the same number of pebbles. Where circles overlap, there is a number giving the sum of the number of pebbles in the two overlapping circles. For example, the number $7$ is in the overlap of circles $A$ and $C$ . This means that the sum of the pebbles in circles $A$ and $C$ is $7$ . Likewise, the sum of the pebbles in circles $C$ and $B$ is $13$ .

Complete the chart and find the number of pebbles in each circle.

Solution

The puzzle diagram gives us the following information:

$A+C=7$ and $C+F = 10$ , therefore $F=A+3$
$B+C=13$ and $C+F = 10$ , therefore $B=F+3$
$D+G=9$ and $G+J = 12$ , therefore $J=D+3$
$G+J=12$ and $H+J = 13$ , therefore $H=G+1$
$H+J=13$ and $E+H = 9$ , therefore $J=E+4$

Note that the letters in the first two lines above are completely different from the letters in the last three lines. Because of this, we can work with them separately. Here, for brevity, we will work out the solution for the first group: $A, C, F, B$ . The technique for the second group is similar. The whole solution is in the figure below, part (1).

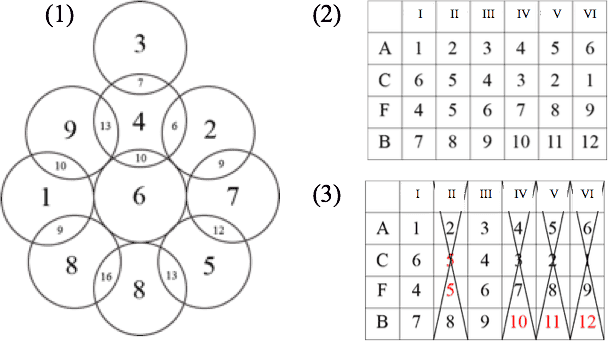
For a problem like this, it helps to chart the letters and their possible values, then narrow down the possibilities. If we start by considering only that $A+C=7$ , then $A$ and $C$ can have values between 1 and 6. Their values then determine $F$ and $B$ . These six possibilities are laid out in the figure, part (2).

Now for the elimination of possibilities. First the possibility II does not work as $C$ and $F$ must be distinct quantities. Additionally, the last three possibilities IV, V and VI do not work, as two-digit numbers aren't allowed. We are left with the two possibilities in the figure, part (3). Nothing more can be done with the first group of letters at this point. To make progress, turn to the second group.

A similar analysis using the non-duplication of numbers and restriction to the numbers 1 through 9, leads, in the case of the second group of letters (that is, $G, D, J, H, E$ ), to four possibilities. Readers can obtain these for themselves using the charting technique already applied to the first group.

Finally, putting the two separate analyses together leads to the unique solution in the figure, part (1).