Ferman Fink was the host at a Valentine's Day party last year. Ms. Phoebe Beebe, a guest, asked Ferman if he had any children. Ferman said, "I have three daughters and I will tell you how old they are. The product of their ages is 72. The sum of their ages is my house number."
Phoebe thought for a few moments. Then she went out and looked at the house number. She came back in and told Ferman that he hadn't given her enough information to solve the problem.
Ferman then said, "OK: my oldest daughter likes vanilla yogurt." Phoebe immediately told him the ages of the three girls.
Can you do the same? (All ages are whole numbers.)
Solution
Discussion: This is a jaw-dropper. Vanilla yogurt? Huh?
Solving the Problem: We must think hard. Phoebe was thinking hard for a few minutes. What could she have been thinking about? Maybe the possibilities. It might be hard to do, but we could make a list of all the possible ages of the three girls, i.e. the possible triples of numbers having product 72. There are lots of them, but some of them would be clearly biologically impossible, e.g. 1, 1, and 72. Maybe that's what Phoebe was doing. And we should do it too. The figure below gives the result with biological impossibilities eliminated. The first three rows are the possible ages of the daughters.
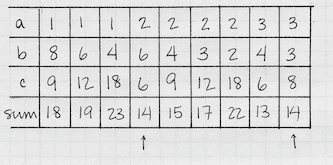
Once the list is made, add up the triples (see the last row of the figure) and have a good look at what you've got. Why couldn't Phoebe give Ferman the answers? Ah – there are two 14's. And how did Ferman's vanilla-yogurt statement help? Ha! It wasn't about the yogurt – he was telling her that he has an oldest daughter. That rules out one of the possibilities, leaving 8, 3, and 3 as their ages.
Heuristics: #11, check all possibilities, and #3, make a chart.
Using the Problem with Students: As we read the problem together, the students will doubtless get off on a tangent about the yogurt. This is fine; let them go. But eventually I'll have to have them to start to work, and either they'll realize that they need a list of possibilities or I can gently steer them in that direction. They may feel that there are just too many possibilities to list, but I ask them what else can we do? Besides, some can be left out as biologically impossible (amusing to identify).
I might help them get the list up on the board, or I might turn them loose on the problem, either as class work or overnight, without giving any further suggestions about adding up the triples or finding out why that information isn't enough.
If the students have worked overnight on the problem, I start the next day's discussion with the table of possible ages on the board – maybe start by having them give them to me. Then we scrutinize it to see what's going on. Eventually someone will see that the difficulty must be that there are two sets of numbers whose sum is 14: 2, 6, and 6, and 3, 3, and 8.
That must be why Phoebe couldn't give the ages: Ferman's house number is 14.
But why vanilla yogurt? Someone will get it: it's not about the yogurt.
Modifying or Extending the Problem: Are there other numbers besides 72 that could be used in such a problem?