A state tennis tournament has 162 players in singles competition. A player plays until he or she loses a match and is then eliminated. If, at any stage of the tournament, there is an odd number of players remaining, one player is given a "bye" and sits out a round. How many matches must be played to determine the tournament champion?
Solution
Discussion: This problem has several interesting facets, the first one being that 162 is a large number to cope with. Second, there are so many ways that players can be matched up that it's hard to see through all of the specifics to spot an underlying pattern. Third, while it's not hard after awhile to come up with a conjecture for the answer, it's another matter to think cleverly and show why the conjecture is correct. This last bit is the main value of the problem.
Solving the Problem: The first step is to invent a diagram showing how a tournament can proceed. This is comfortably done by using a small number of players and drawing the way the tournament might look, as shown in two examples in the figure below.
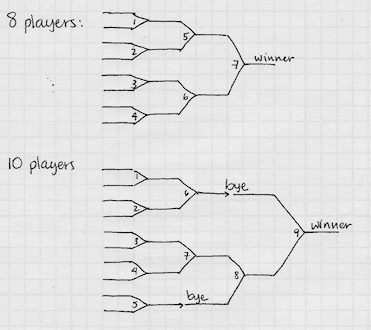
If we count up the number of matches needed in each of the three drawings, a conjecture presents itself immediately: for players, matches are needed. This can be verified by taking more examples, with different numbers of players.
But why will it always work? What lets us say with confidence that for 162 players, 161 matches will be needed?
A bright idea surfaces – an "aha" moment: the tournament is producing not only 1 winner, but is also producing 161 losers. And it takes one match to produce one loser, so there must be 161 matches.
Heuristics: We use #5, draw pictures; and #14, make simpler versions, and #7, look for patterns. But the biggie is #16: look at the problem in a new way.
Using the Problem with Students: I most often use this problem as a demonstration of "thinking out of the box". It's an easy problem to present. In class I'll have different students draw up diagrams for different numbers of players, and then making a simple table on the board: number of players and number of matches, brings the conjecture out into the open right away. If students feel comfortable with the conjecture I'll remark that OK that's good science but it's not good mathematics until we can prove what we assert. So then I have to goad them to think cleverly: "We know that the tournament with 162 players will produce one winner. But what else will it produce?" (161 losers.) And how many matches does it take to produce a loser? (one!) Aha! So... ?
Modifying/Extending the Problem: Stella isn't familiar with other forms of elimination tournaments, with, for instance, consolation rounds. Students who have their heads into such things might like to devise similar problems with different parameters. The NBA basketball championships might lend themselves to analysis – don't the newspapers have fill-in charts?