The object of this problem is to connect each utility line (gas, electricity, and water) to each of the three houses without crossing lines. The paths can be as long and as convoluted as necessary, so long as they don't cross (or pass under, over, or through a house or other utility line). Can you solve the problem? If not, can you prove that nobody can?

Solution
This is a classic result in Graph Theory: the complete bipartite graph is not planar. In ordinary English: two groups of three points cannot be connected, each point of one group with each point of the other group, while staying in a plane. You can make 8 of the 9 connections that are needed (see the figure below) but the last one will always be out of reach, that is, requires the third dimension to complete.
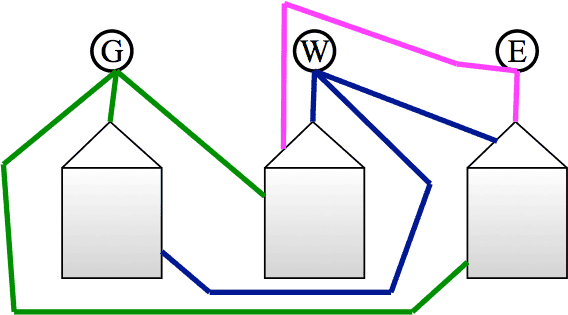
The proof is not easy. In almost every class there is someone who, quite properly, doubts the impossibility of a solution. It is good to let them try to solve it to their heart's content.