1020.23 – Vacation on a Triangular Island

You are camping on the equilateral island of Gelyksydig in the Indian Ocean off the coast of South Africa (see the figure below). All three sides are terrific beaches. Where should you camp so that the sum of the straight line path to the three beaches is as small as possible?

Draw your own map of the island and experiment by plotting a few points and measuring with a ruler the sum of the straight line paths. Keep track of this sum for your choice of points. Then formulate a conjecture and prove it.

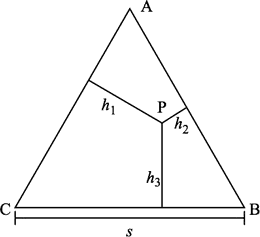
Solution

You can camp anywhere. Consider the point P, for example, in the figure below. Then the distances, $h_1, h_2, h_3$ , are altitudes of the sub-triangles respectively $\triangle APB, \triangle ACP, \triangle BCP$ . This means that the areas are

\begin{aligned} \triangle ABP &=& \frac{1}{2} AB \cdot h_3 = \frac{1}{2} BC \cdot h_3, \\ \triangle ACP &=& \frac{1}{2} AC \cdot h_2 = \frac{1}{2} BC \cdot h_2, \\ \triangle BCP &=& \frac{1}{2} BC \cdot h_1 = \frac{1}{2} BC \cdot h_1 \end{aligned}

Adding gives

$\frac{1}{2} BC \cdot (h_1 + h_2 + h_3) = \triangle ABC = \frac{1}{2} BC \cdot h.$

Thus

$h_1 + h_2 + h_3 = h$

and we see that the sum of the distances to the three beaches is the altitude of the triangle regardless of where P is.

p.s. "Gelyksydig" is "equilateral" in Afrikaans.