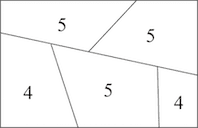
The figure represents the design of a very modern beach house. The goal of this puzzle is to trace a path that crosses each of the 16 wall segments once and only once. It is, in fact, impossible, but can you prove it?
Hint: Consider the number of wall segments in each ‘room’. Where is the path supposed to begin and where is it to end?
Solution
Here the number of wall segments has been added to each room. There are three rooms with five segments. Such a room can only be the start or the end of the path because it has an odd number of wall segments. Since there are three such rooms, the supposed path has the begin and end in three rooms and that is impossible.