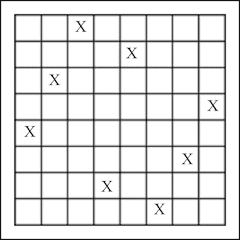
Pretend that the grid below is a chess board. Your job is to place eight queens on the board in such a way that no queen can capture any other queen.
For those who don’t play chess, what you need to do is fill in eight of the sixty-four squares below so that no two squares are in line with each other vertically, horizontally, or diagonally.

Solution
There are ninety-two different ways to arrange the queens, but most of them are really just reflections or rotations of each other. There are twelve fundamentally distinct solutions to this puzzle. See how many you can find! Here is just one: