Scott the painter is going to paint the floors of sixteen rooms. See the diagram?
Scott is in room 1. He can go through any door. See the doors? He can't return to any room once he has painted it: slow-drying paint! In what order should he paint the rooms? Obviously, #16 must be last.
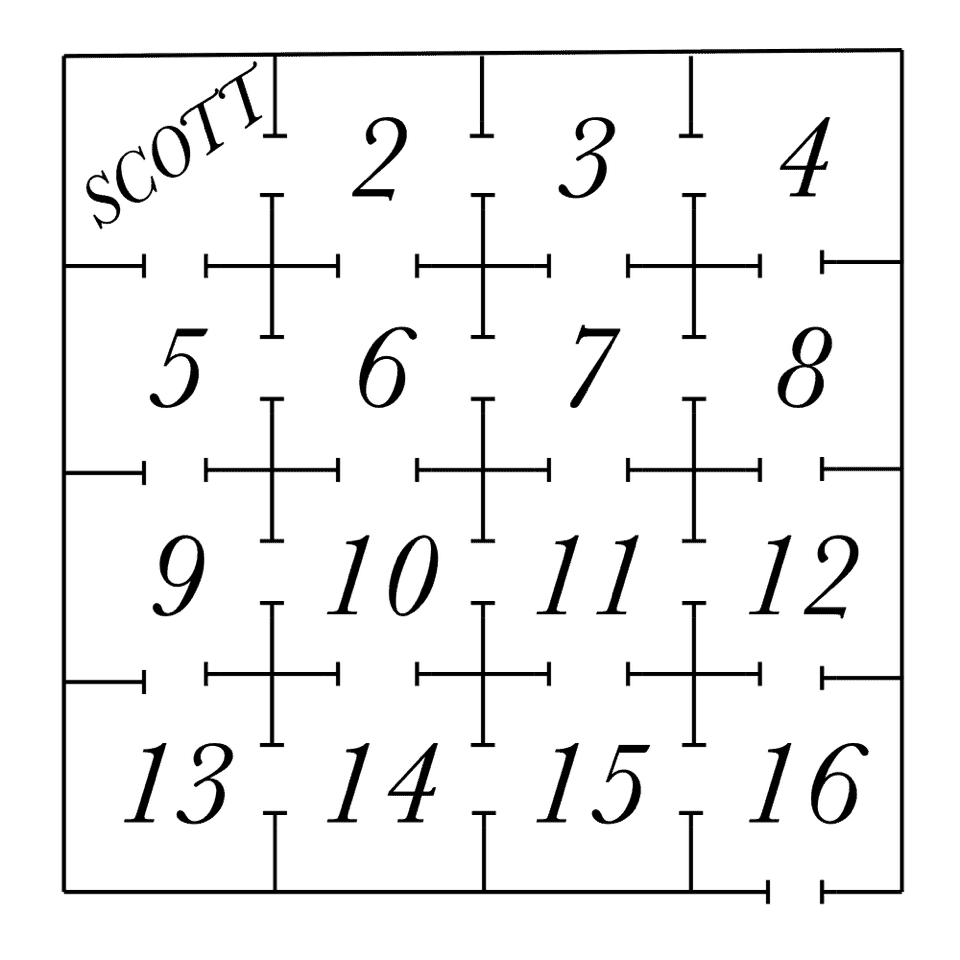
Solution
Discussion: This is an obvious guess-and-try problem, but its value is in teaching us not to assume too much.
Solving the Problem: If we try it a few times, or a lot of times, we find no success. And this will continue to be the case until we realize that we are making an unnecessary assumption, namely that Scott has to paint room #1 first. Try having him start someplace else.
Heuristics: #2, guess and try, and #17, check for hidden assumptions.
Using the Problem with Students: This problem's task is easily understood, and students are willing to dig in on it. If students are working on it in class, I'm ready for somebody to blurt out the question, "Does he have to start in room 1?", and that gives the game away – which is OK with me. The point is for students to see that they need to be on the watch for unnecessary assumptions, and if that gets brought out very soon, it's OK.
Modifying or Extending the Problem: This problem goes very fast, and once students see that they can start in rooms other than #1, it's natural to extend the problem right away. The question is, which rooms can Scott begin with so that he can paint them all, and which rooms won't work as starters? There's a pattern to be found, and some thinking to do about why that pattern works. (Stella would like to hear from anyone with a reason for this.)
A further extension is possible: What if there aren't 16 rooms, but 9, or 25, or some other perfect square? What if the room is rectangular?