This funnel was devised by an ancient king to determine which of his captives should die. The funnel contains both white sugar pills and black poison pills. Pressing the button at the bottom causes one pill to fall out.
Each captive is forced to press the button and allow the first pill to fall into his hand. He must then replace that pill into the top of the funnel, press the button again to obtain a second pill, and swallow that pill regardless of its color. Turn then passes to the next captive.
Using this information and the diagrams below, answer the following questions:
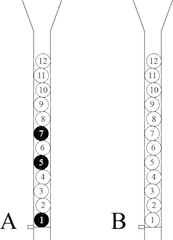
Scenario A shows that twelve pills are ready to be drawn by nine captives. Captive 1 will draw and replace Pill 1 before eating Pill 2. Captive 2 will draw and replace Pill 3 before eating Pill 4. This pattern continues until every captive has taken a turn. Which captive(s) will die?
Scenario B also shows that twelve pills are ready to be drawn by nine captives, but, this time, there are no poison pills. Assuming that the same pattern of drawing, replacing, drawing, swallowing, and passing the turn continues, which three pills should you poison to ensure that each of the captives survives his first turn?
Solution
Captive 8 will be the first to swallow a poison pill. Should the pattern continue until all the pills are eaten, Captive 1 and Captive 2 will die as well.
Pill 1, Pill 5, and Pill 9 should be poisoned if all captives are to survive at least one turn.