3420.29 – Midline Triangle

In a random triangle △ABC\triangle ABC, DD is the midpoint of ABAB, EE is the midpoint of BDBD, and FF is the midpoint of BCBC.

Suppose the area of △ABC\triangle ABC is 9696. Then the area of △AEF\triangle AEF is:

  1. 1616

  2. 2424

  3. 3232

  4. 3636

  5. 4848

Solution

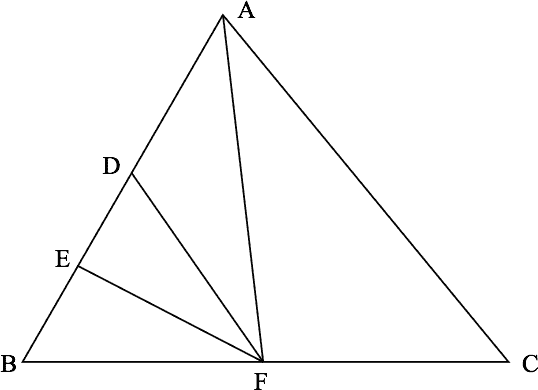
The figure described in the problem is drawn above. Note that if you halve the base of a triangle and don't change the altitude, you halve the area. Therefore,

△ABC=96△ABF=48 (base being halved: BC)△ADF=24 (base being halved: AB)△BDF=24 (base being halved: AB)△DEF=12 (base being halved: BD)△AEF=△ADF+△DEF=24+12=36\begin{aligned}\triangle\text{ABC} &= 96 \\\triangle\text{ABF} &= 48 \ (\text{base being halved: BC)}\\\triangle\text{ADF} &= 24 \ (\text{base being halved: AB)}\\\triangle\text{BDF} &= 24 \ (\text{base being halved: AB)}\\\triangle\text{DEF} &= 12 \ (\text{base being halved: BD)}\\\triangle\text{AEF} &= \triangle\text{ADF} + \triangle\text{DEF} \\&= 24 + 12 \\&= 36\end{aligned}